Коллеги - педагогический журнал Казахстана
Учительские университеты
| Главная » Статьи » В помощь учителю » Математика |
Методика доказательства теорем
| Среди всех методов доказательства теорем в школьном курсе геометрии основную нагрузку несет синтетический метод, ибо он является составной частью доказательства любым другим методом. Анализ и синтез практически неотделимы друг от друга и составляют единый аналитико-синтетический метод. Мы их рассмотрим в отдельности друг от друга, чтобы наиболее выпукло показать особенности каждого метода. Доказательство математического предложения х М: А (х) =В (х) называется синтетическим, если оно осуществляется по следующей логической схеме: (А(х) Т) В1 (х) В2 (х) ... Вn, (х) В (х), где Т — определенная совокупность предложений той математической теории, в рамках которой доказывается данное предложение и которой принадлежат В1 (х), В2 (х), ..., Вn, (х), составляющих доказательство, а также суждения А (х) и В (х). Таким образом, при синтетическом методе доказательства теоремы цепочка силлогизмов строится так, что мысль движется от условия теоремы к ее заключению. Рассмотрим синтетическое доказательство теоремы о сумме внутренних углов треугольника. Д а н о: АВС — треугольник (рис. 1). Доказать: = 1800. Доказательство: 1) Проведем через вершину В прямую а, параллельную АС. 2) Рассмотрим 1 и 4; они являются накрест лежащими углами при пересечении параллельных прямых а и АС и секущей АВ, а значит, 1= 4. 3) Рассмотрим 3 и 5; они накрест лежащие при пересечении параллельных прямых а и АС и секущей ВС, а значит, 3= 5. 4) Сумма 4, 2, 5 равна развернутому углу с вершиной В, т.е. 4+ 2+ 5=1800. 5) Значит, 1+ 2+ 3= 1800. Теорема доказана. рис. 1 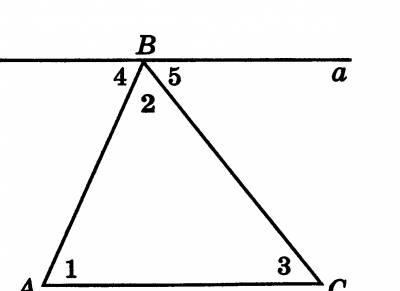 К достоинствам синтетического метода следует отнести сжатость, краткость, исчерпывающую полноту, логическую безупречность образца рассуждений. В методическом отношении синтетический метод имеет и свои недостатки: для учащихся остается неясным, как можно обнаружить такое доказательство, почему в рассуждениях поступают так, а не иначе; не аргументируется, почему нужны те или иные дополнительные построения; школьники не представляют, в каком направлении должны протекать рассуждения, так как этому методу свойственна большая неопределенность и многозначность при выборе пути доказательства теоремы. Перечисленные недостатки отрицательно сказываются на развитии у учащихся продуктивного, творческого мышления. При аналитическом доказательстве теоремы х М: А (х) =В (х) цепочка силлогизмов строится так, что мысль движется от заключения теоремы к ее условию. Различают два вида аналитического метода: восходящий анализ (анализ Паппа), нисходящий анализ (анализ Евклида). Восходящим анализом (совершенным анализом) называется такая разновидность аналитического метода, при которой, отталкиваясь от заключения, подбирают для него достаточное условие — такое суждение В1 (х), что В1 (х) В (х), затем подбирают достаточное условие В2 (х) для В1 (х), такое, чтобы В2 (х) В1 (х) было истинным, и так далее до тех пор, пока не получат такое достаточное условие Вn(х) для Вn-1(х), что Вn(х) Вn-1(х) и Вn (х) выполняется (истинно). При этом используется как условие А(х) доказываемого предложения, так и некоторая совокупность Т связанных с А (х) и В (х) предложений данной теории, истинность которых уже была установлена. Сущность метода восходящего анализа состоит в том, что рассуждения строятся по схеме: для того чтобы В (х) было верно, достаточно, чтобы было верно С (х), и т. д. Рассмотрим доказательство теоремы методом восходящего анализа. Т е о р е м а: Диагонали ромба взаимно перпендикулярны». Доказательство: 1) для того чтобы доказать, что АС ВD (рис. 2), достаточно доказать, что ВО АС. 2) для того чтобы доказать, что ВО АС, достаточно доказать, что ВО — высота треугольника АВС. З) для того чтобы доказать, что ВО является высотой треугольника АВС, достаточно доказать, что треугольник АВС раннобедренный и ВО в нем является медианой. 4) для того чтобы доказать, что треугольник АВС равнобедренный, достаточно доказать, что в нем АВ = ВС. 5) Но АВ = ВС по условию (АВСD — ромб) и ВО — медиана треугольника АВС (так как АО = ОС по свойству диагоналей параллелограмма). рис. 2 Теперь, идя обратным путем, от пункта 5 к пункту 1, мы и докажем сформулированную теорему. Нисходящим анализом (несовершенным анализом) называют такую разновидность аналитического метода, при которой, отталкиваясь от заключения В (х) доказываемого предложения А (х) В (х), рассуждения ведут путем последовательного получения логических следствий: В(х) В1(х) В2(х) ... Вn, (х), где Вn(х) есть предложение, истинное значение которого нам точно известно. При выведении следствий из В(х) временно допускают, что оно истинно. При нисходящем анализе, так же как и при восходящем, рассуждения ведут от заключения теоремы, но подбирают уже не достаточные, а необходимые условия. При использовании нисходящего анализа возможны два основных случая. Следствие Вn(х), полученное из В(х), истинно. В этом случае об истинности доказываемого предложения А (х) В (х) ничего нельзя сказать, так как из ложного предложения может следовать и истинное. Например, из ложного предложения ( , ) следует истинное предложение ( ). Но в том случае, когда применение нисходящего анализа к доказательству теоремы х М: А(х) В (х) приводит к следствию Вn(х), которое истинно, целесообразно попытаться обратить этот аналитический процесс рассуждений в синтетическое доказательство: (В(х) (А(х)) Вn-1(х) ... В1(х) В(х) В таком случае нисходящий анализ позволит нам отыскать путь синтетического доказательства. Для примера рассмотрим доказательство теоремы: «Если в четырехугольнике противоположные стороны попарно равны, то четырехугольник - параллелограмм. Доказательство: 1) Пусть АВСD - параллелограмм (рис. 3). (В (х)) рис. 3 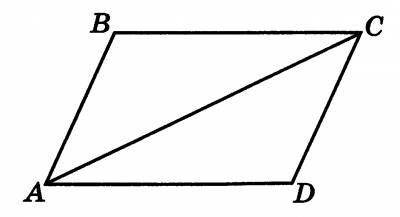 2) Тогда ВС АD и АВ DС. (В1(х)) 3) Тогда АСВ= САD, ВАС= АСD) (как накрест лежащие углы при параллельных прямых и секущей). (В2(х)) 4) Из равенства этих углов с учетом того, что АС — общая сторона треугольников АВС и АDС, следует: АВС = АDС. (В3(х)) 5) Тогда АD=ВС, АВ=DС, АС=АС. (А(х)) Итак, имеем В(х) В1(х) В2(х) В3(х) А(х), где А(х) — истинно. Проведя теперь рассуждения в обратном порядке А(х) В3(х) В2(х) В1(х) В(х), мы получим синтетическое доказательство. Следствие Вn(х), полученное из В(х), ложно, тогда всегда ложно и само В(х). Этот случай нисходящего анализа используется и для доказательства от противного. Так, чтобы доказать истинность предложения А(х) В(х), преобразуют его в предложение А(х) и к доказательству последнего применяют метод нисходящего анализа. Если следствие В(х) окажется ложным, то этим будет доказана ложность предложения А(х) В(х), а это, в свою очередь, доказывает истинность А(х) В(х). Рассмотрим примеры доказательств методом нисходящего анализа (в данном случае мы используем метод доказательства от противного). Т е о р е м а: Разносторонний треугольник нельзя разбить на два равных треугольника. Доказательство: 1) Пусть АВМ= ВМС (рис. 4), АВ ВС АС. 2) В этих равных треугольниках ВМ общая сторона и по теореме о том, что в равных треугольниках против равных сторон лежат равные углы, заключаем, что ВАМ = ВСМ. З) По теореме о том, что если углы при основании треугольника равны, то треугольник равнобедренный, заключаем, что АВ=ВС. 4) Мы получили, что АВ = ВС, но по условию теоремы АВ ВС. Получили противоречие. 5) Значит, наше предположение неверно, а верно то, что АВМ ВМС С рис. 4 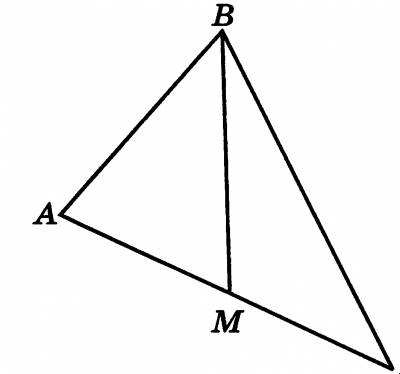 Доказательство методом исключения строится на конструкции исключения, к которой затем применяется метод противоречия. Если нужно доказать теорему х М: А(х) В(х) методом исключения, то наряду с заключением В(х) рассматривают все остальные возможности: В1(х), В2(х), ..., Вn (х). Затем предполагают, что вместо заключения В(х) имеет место В1(х), и показывают, что это приводит к противоречию. Так поступают и со всеми остальными возможностями: В2(х), ..., Вn(х). В результате остается лишь одна возможность: х М: А(х)=В(х). Обычно такой метод доказательства применяется там, где нужно использовать аксиому трихотомии (для любых чисел и возможно одно из трех: ). Рассмотрим теорему: В треугольнике квадрат стороны, лежащей против острого угла, меньше суммы квадратов двух других сторона. доказательство этой теоремы можно провести методом исключения. Вначале предположим, что квадрат этой стороны равен сумме квадратов двух других сторон, и получим противоречие; затем предположим, что квадрат этой стороны больше суммы квадратов двух других сторон, и опять получим противоречие; эти два противоречия позволяют заключить, что возможно только одно: квадрат стороны, лежащей против острого угла треугольника, меньше суммы квадратов двух других сторон. Перейдем к рассмотрению доказательства теорем методом перебора. Этот метод — один из древнейших методов, которым пользуются и в современной математике. Хотя теоремы в абсолютном большинстве распространяются на бесконечное число объектов, в математике имеют место и такие теоремы (задачи на доказательство), которые охватывают лишь конечное число объектов. для доказательства таких теорем можно использовать метод перебора. Так, например, для того чтобы доказать, что среди двузначных чисел есть только два числа, которые равны утроенному произведению их цифр, можно перебрать все двузначные числа от 10 до 99 и показать, что требованию теоремы удовлетворяют лишь числа 15 и 24. Обратим внимание читателя на одно важное обстоятельство. При использовании метода перебора следует, прежде всего, посредством рассуждений несколько сузить область значений, подлежащих рассмотрению, т. е. следует, имея заведомую возможность найти решение полным перебором всех вариантов, вначале поломать голову, чтобы каким-либо образом ограничить количество вариантов. Проиллюстрируем вышесказанную мысль на такой задаче: «Доказать, что среди двузначных чисел есть только одно, которое равно удвоенному произведению его цифр». Доказательство: В соответствии с условием задачи мы должны найти двузначное число , для которого выполняется равенство , т. е. . Выразим из последнего равенства: Учитывая, что - это цифра, можно записать: . Из равенства следует, что . Таким образом, из системы следует: . Хотя перебор всех натуральных значений , удовлетворяющих неравенству , не сложен, но можно еще сузить область перебора, для этого заметим, что должно быть четным. Тогда следует рассмотреть лишь =6, =8. Итак, проведенные рассуждения позволили сузить область перебора от 90 до 10 случаев, затем до 4 и окончательно до 2 случаев. При =6 цифрой а будет 3, а числом будет 36. Это число удовлетворяет требованию задачи. При =8 значение а будет дробным числом, но так как а — это цифра, то а дробным быть не может. Итак, мы получили, что лишь одно двузначное число 36 равно удвоенному произведению его цифр. Доказательство теоремы методом полной индукции строится следующим образом: перебираются все возможные случаи, к каждому из которых применяют либо синтетический метод, либо метод противоречия. Примером может служить доказательство теоремы об измерении вписанного угла половиной дуги, на которую он опирается. Доказывая эту теорему методом полной индукции, мы должны рассмотреть все три возможных случая: центр окружности лежит на стороне вписанного угла, центр окружности лежит между сторонами вписанного угла, центр окружности лежит вне вписанного угла. Итак, суть метода полной индукции заключается в том, что, общее утверждение доказывается по отдельности в каждом конкретном случае из числа тех, которые могут представиться. Более глубокому пониманию сути метода полной индукции будет способствовать решение таких задач, которые аналогичны следующей: Доказать, что решениями неравенства х18 - х15 + х2 - х + 1>0 будут все действительные числа. доказательство Разобьем числовую прямую на три промежутка: а) х<0; б) 0<х<1; в) х>1. докажем, что на каждом из этих промежутков неравенство выполняется. Если х<0, то первые четыре слагаемых, стоящие в левой части неравенства, неотрицательны, а 1 больше нуля, а значит, их сумма больше нуля. При 0<х<1, группируя члены, стоящие в левой части неравенства, следующим образом: х18 + (х2 — х15) + (1— х)> 0, мы будем иметь, что все слагаемые положительны, а значит, их сумма больше нуля. Если х>1, то группировку слагаемых проведем следующим образом: (х18 — х15)+(х2 — х)+ 1>0. При х>1 первые два слагаемых неотрицательны, а единица положительна, и, значит, вся сумма больше нуля. Заметим, что речь в этой задаче шла о бесконечном числе случаев (х R) и перебрать их все не представляется возможным. для того чтобы использовать метод полной индукции, мы разбили бесконечное число случаев на конечное число вариантов (здесь основой разбиения служит смена знака выражения), а затем каждый вариант рассматриваем в отдельности. Абсолютное большинство математических предложений охватывает бесконечное множество частных вариантов, и провести проверку истинности этих предложений в таком случае путем перебора или путем разбиения этого бесконечного множества на конечное число подмножеств мы не можем. Тогда во многих случаях обращаются к особому методу доказательства — методу математической индукции. Суть этого метода доказательства состоит в следующем. Пусть требуется доказать справедливость некоторого утверждения для любого натурального числа n. Чтобы доказать это утверждение, проверяют его справедливость для n =1. Затем доказывают, что при любом натуральном значении k из справедливости рассматриваемого утверждения при n = k вытекает его справедливость при n = k +1. Тогда утверждение считается доказанным для всех n N. Когда принцип математической индукции (его иногда называют аксиомой арифметики натуральных чисел) используют для доказательства теоремы ( n N) (А (n)), то фактически строится такой силлогизм: Большая посылка: принцип математической индукции. Малая посылка: А(n), n N: А(1) — истинно; (А(k) А(k+1)) — истинно. Вывод: А(n) — истинно для любого натурального n. Когда нужно доказывать справедливость некоторого утверждения не для всех натуральных чисел, а лишь для n р, где р — фиксированное натуральное число, то в этом случае пользуются принципом математической индукции, сформулированным следующим образом: .Если предложение истинно при n =р и из его истинности при n =k, где k р, следует, что оно истинно и при n = k +1, то предложение истинно для любого n р Докажем методом математической индукции истинность равенства 1+3+5+... +(2n - 1)=n2. (*) 1) При n =2 (мы взяли базу индукции для n =2, а не для n =1, ибо доказывается формула для суммирования) доказываемое равенство принимает вид 1+3=22, которое истинно. Итак, равенство (*) истинно при n =2. 2) Предположим, что равенство (*) истинно при n = k, т. е. справедливо равенство 1+3+5+... +(2k-1)=k2. докажем, что тогда равенство (*) истинно и при n =k +1, т. е. справедливо равенство 1+3+5+... +(2k-1)+(2k+1)=(k+1)2. Преобразуем левую часть последнего равенства: 1+3+5+... +(2k-1)+(2k+1)=(1+3+5+... +(2k-1))+(2k+1). Но по предположению индукции сумма, стоящая в первой скобке последнего равенства, равна k2. Значит, вся сумма равна k2+2k+1=(k+1)2. Итак, имеем 1+3+5+... +(2k-1)++(2k+1)=(k+1)2. Тем самым по принципу математической индукции истинность равенства (*) доказана для любых n N. Получается равенство (*). На случай бесконечного числа возможных вариантов в математике используется еще один метод доказательства. Его суть состоит в следующем. Математическое утверждение доказывается для конечного числа случаев, и делается вывод о невыполнимости этого утверждения для остальных случаев, которых бесконечное число. Назовем этот метод доказательства методом бесконечных исключений. Рассмотрим пример, иллюстрирующий этот метод доказательства. Доказать, что если длины сторон прямоугольника выражены натуральными числами, причем числовое значение его периметра равно числовому значению его площади, то таких прямоугольников может быть только два. Доказательство: Обозначим длины смежных сторон прямоугольника через х и у. По условию ху =2 х +2 у. Из уравнения имеем у = . Выделим целую часть у полученного выражения: у= = = . Так как по условию х и у натуральные числа, то сумма может быть числом натуральным лишь при х=3, х=4, х=6. При всех остальных числах эта сумма не может быть числом натуральным. Соответствующие значения для у будут у =6, у=4, у=3. Очевидно, что различных решений два: прямоугольник со сторонами 3 и 6 и квадрат со стороной 4. Суть метода конструирования состоит в том, что путем геометрических построений, основанных на свойствах геометрических фигур, известных определениях и теоремах, строится объект, о котором идет речь в математическом утверждении. Построение указанного объекта на плоскости производится путем определенного набора инструментов и опирается на постулаты построения, т. е. на элементарные задачи на построение; построение объекта считается выполненным, если оно сведено к конечному числу этих задач-постулатов. Этим методом в школьном курсе геометрии доказаны, например, теорема о существовании и единственности окружности, описанной около треугольника, теорема о существовании и единственности окружности, вписанной в треугольник, теорема о касательной к окружности. Источник: http://Совершенствование методики работы учителя математики : Кн. для учителя / Я. И. Груденов . – Москва : Просвещение, 1990 | |
| Просмотров: 6483 | |
Понедельник, 2025-07-14, 4:34 PM
Приветствую Вас Гость
Приветствую Вас Гость
Форма входа |
|---|
Социальные закладк |
|---|
Поиск |
|---|
Друзья сайта |
|---|
Теги |
|---|
Статистика |
|---|